第四章 ACES 预备课——灰灰的就是 log?
- Color
- 十分钟系列
第四章 ACES 预备课——灰灰的就是 log?
4.1 gamma 本质是什么?
gamma 很神奇。
很多人喜欢她
很多人讨厌他。
有人觉得gamma 是亮度
有人觉得gamma 是显示器的特性
有人觉得gamma 是曲线
有人觉得gamma 是2.2……
这些都是gamma,也都不是gamma……
gamma 其实很简单,就是个指数而已。
千万别一看到公式就脚软,其实很简单的!
相信大家都会算 $ y = x^2 $ 对吧?
那么 x 头顶上面的那个2 就是gamma。
如果 gamma = 1?
岂不就是 y = x !
我们来看看为什么要有gamma 呢?
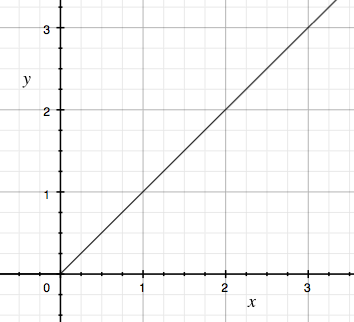
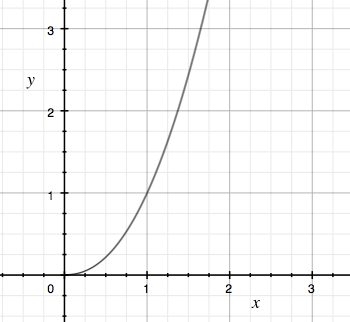
先来对比一下一维的图像,横坐标是输入,纵坐标是输出。
不断的给出x 的数值,就可以得到对应的 y。
很明显,y = x 就是一条直线,这就是我们传说中的 “linear” 。(这是科普文章,千万不要过度的讨论“线性” 的定义,那可就深了……)
y = x,要怎么理解呢?肯定很多人就会说:“输入和输出相同啊!”。
没错,不过这是第一层含义,更重要的含义是:“输入的间隔与输出的间隔相等。”
这是什么意思?
在计算机里面,所有的数据都是有离散的,也就是输入的数据都是间隔的。
比方说,我每间隔 0.001 输入一个x,那么y 的间隔肯定也是0.001。
就好像上面图片(y = x 那个)中 x 在 0~1 的范围之间有五个采样点,间隔0.2;对应 y 的间隔也是0.2。
但是对于 $ y = x^2 $ 来说,x 在 0~1 的范围之间也有5个采样点,间隔0.2;但是对应y 之间的距离却是不相等的。
使用gamma 可以在图像存储上更有效率的利用存储空间。
因为人眼对暗部的细节更加敏感,如果同样是8 bit 的存储空间,我花费更多的6 bit 来记录暗部的数据,会得到更好的效果——简称:更值得!
如果采用线性记录,那么所有范围的信息都会平均的记录到8 bit 上,假设有4bit 记录了亮度,4 bit 记录了暗部,由于人眼对于亮部不敏感,所以这部分的空间就显得有点浪费——简称:不值得!。
这就是为什么在“很久”以前,计算机能力还没有现在这么夸张的年代,很多图像都采用 log 对数方式记录,为的就是把有限的记录空间用到人眼敏感的范围上。
当然了,由于现在计算机处理能力大幅增长,存储空间和计算都显得不是那么拮据,linear 的优势显现出来,openEXR 16 bit float linear 存储的图片格式也就越来越常见了。
(感觉好像当你穷的只有10块钱的时候,明明知道汽车方便,但是为了生存还是先买两个馒头吧。之后有钱了,就无所谓了,高兴就买两辆跑车…… )
4.2 色度的gamma
一维的gamma 说完了,我们来进化一下,变成二维!
先回忆一下,上一次说到的三角形切分对应gamma 的概念。(这里更细致的区分色度:二维和色域:三维)
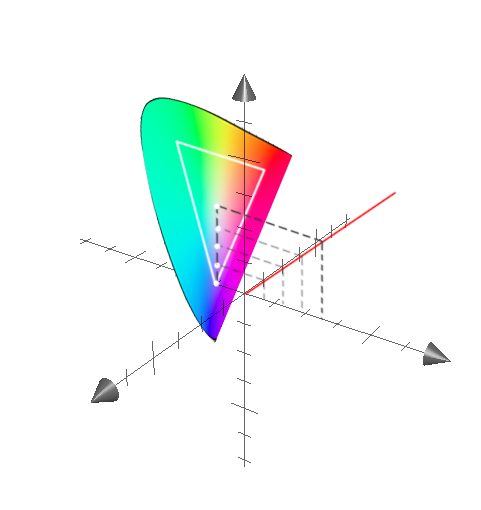
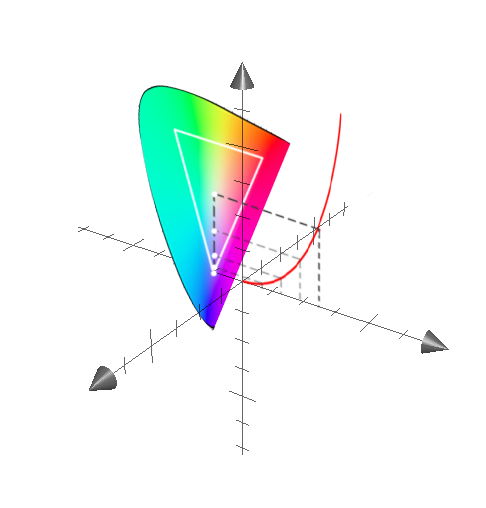
红色的线就是对应刚刚说到的曲线。
(不要吐槽绘图、不要吐槽色彩空间位置,这些是为了说明对应关系而已)
先来看上边的图,y = x 的重要特性就是 “输入的间隔 与 输入的间隔 相等”。
我们的曲线等距的进行五次采样,对应的y 我们正好投射到顶点与白点之间的连线上,可以看到五个白点之间的间隔也是等距的。
如果我们分别对三个基色进行三次这种的操作,那么每个基色到白点之间的采样点,都是等距的。然后再依此连接这些采样点,就形成了上次说过的等距切分的三角形。
再来看下边 $ y = x^2 $ 的采样。同样的,我们的输入还是等距的,但是对应 y 的间隔却是越变越大的。我们也对三个基色进行三次这样的操作,结果就得到了外围切分的很细,越靠近白点切分的越粗的切分三角形。
这就是二维中gamma 的表现形式。可以粗略的认为是不是等距离的向内切分。
4.3 向三维色彩空间进发!
色彩空间,他是一个空间!空间就是三维的!所以色域是一个体积!
还记得上次说过的定义色彩空间的时候,我给出了**“至少” 三个条件**:
- 基色
- 白点
- gamma
这三个在色度图上完整的定义了一个三角形的位置、面积、中心点、采样间隔。那么如果把三角形变成立体的呢?就是亮度!
亮度可以决定了这个三角形可以有多高。有了亮度,我们终于定义了一个完整的色彩空间!
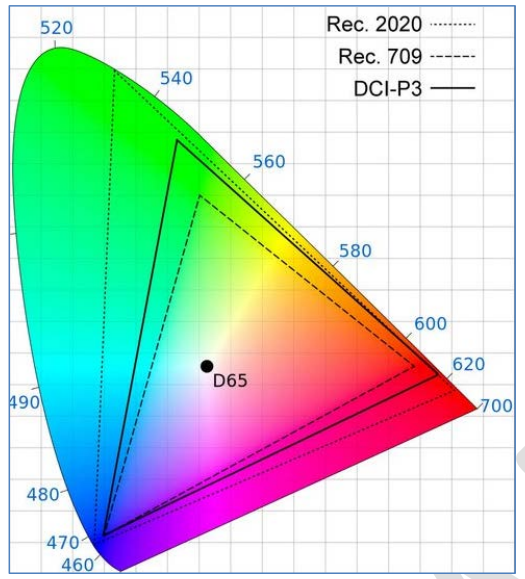
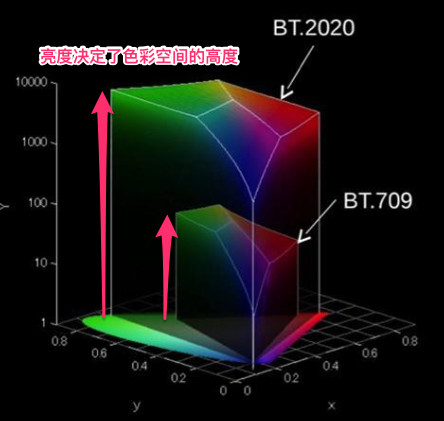
来看看这个例子,大家都知道Rec 709 是高清电视的色域,而下一代HDR 电视机要使用的是Rec 2020 色域。
如果仅仅从色度上面来看,Rec 2020 是比Rec 709 大了一些。
但是如果我们加入亮度的考虑,那么实际上Rec 2020 可以呈现的色彩可是要比Rec 709 大出好多啊!
(现在认为1000 nit 是比较不错的HDR 显示设备,2000 nit 非常好,4000 nit 只有Dolby 自家的Pulsar……对不起,你买不到的。)
现在我们还是重复上面的操作,但是除了三个基色之外,我们再加上亮度:
- 对三个基色到中心点进行等距切分
- 对亮度,从最亮到最暗进行等距切分
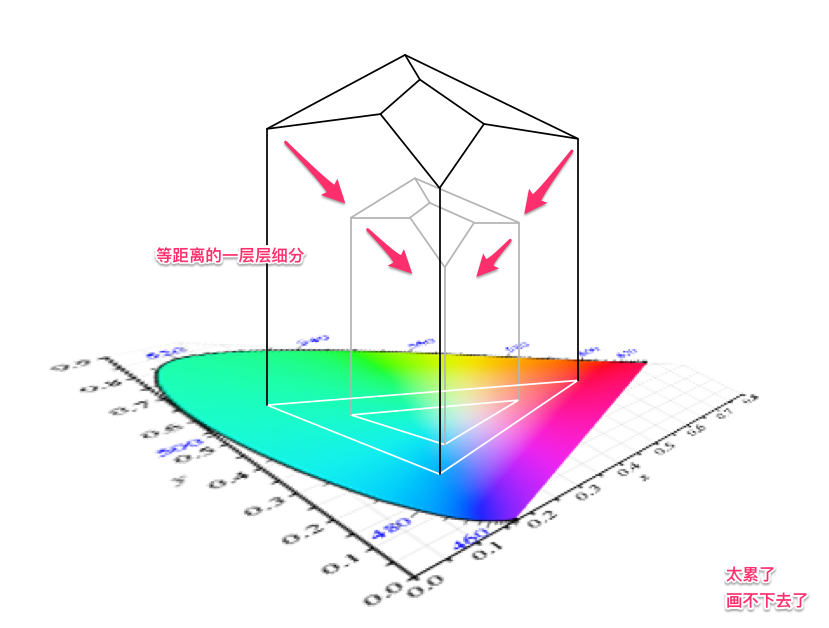
这时候,我们好像把整个色彩空间的体积进行一层层的细分。
每层细分之间都是等距的。
于是就得到了下面的感觉:
(我只画了一层……太麻烦了,大家开动一下想象,总之就是等距的一层又一层)
4.4 总结
简单来说,gamma 就是一个采样的分布。
如果所有因素(色度、亮度)的采样都是等距的,那么这个色彩空间的gamma = 1。也就是很多软件里面指的linear。
相反,如果不是等距的,大部分情况下都是为了更有效的利用存储空间,采用 log 方式进行采样。我们经常听到:
看起来灰灰的图像,是 log 的……
这句话虽然我也一直说,但是心里总是有点别扭。
因为种种历史原因,大家常说的 log 其实是指 cineon log。
在胶片年代,的确只要看起来灰灰的图像,基本都是 cineon log,于是被很多人简称为 log。然后流传至今。(怀念kodak 一秒钟)
但是现在数字摄影机大行其道,感光元器件的性能和胶片大不一样,每家厂商都觉得需要改进一下“log” 让他能在有限的存储空间内,更有效的记录最有用的部分,于是就有了:
LogCRedLogfilmSlog1/2/3ClogDlogACESccACEScct- ……
这些图像都看起来灰灰的,但是他们都不是传统的 cineon log。
所以最后也希望大家能够准确的说明 log 的类型。
这样才不会出现制作中的各种问题 + 扯皮……
A:“做完了,你要什么样子输出给你?”
B:“Log 的就行”
A:“哪种Log?”
B:“就是灰灰的那种!”
A:“所以说,你到底要的是哪种Log……?”
B:(OS:这哥们连 log 都不懂?)“算了,怎么给你的,怎么还给我……”
A:(OS:早说嘛,就是要个
WideGamut-LogC的嘛)“恩, 好的”

